. Рассмотрим первое неравенство: 10,4х1 + 16х2 ≤144

Для начала построим прямую l1 : 10,4х1 + 16х2 =144

Находим две любые точки, принадлежащие прямой.

Пусть х1 = 0, тогда х2 = 9. Получили точку (0;9)

Пусть х2 = 0, тогда х1 = 13,8. Получили точку (13,8;0)

Чтобы узнать, какую полуплоскость - верхнюю или нижнюю по отношению к прямой - задает неравенство, подставим в неравенство значение какой нибудь точки. Например (0;0) : 10,4*0 + 16*0 = 0, 0 ≤ 144, т.е. берем ту полуплоскость, которая содержит (0;0), т.е. нижнюю.

. Рассмотрим второе неравенство: 4х1 + 2х2 ≤30

Для начала построим прямую l2 : 4х1 + 2х2 =30

Находим две любые точки, принадлежащие прямой.

Пусть х1 = 0, тогда х2 = 15. Получили точку (0;15)

Пусть х2 = 0, тогда х1 = 7,5. Получили точку (7,5;0)

Чтобы узнать, какую полуплоскость - верхнюю или нижнюю по отношению к прямой - задает неравенство, подставим в неравенство значение какой нибудь точки. Например (0;0) : 4*0 + 2*0 = 0, 0 ≤ 30, т.е. берем ту полуплоскость, которая содержит (0;0), т.е. нижнюю.

. Рассмотрим третье неравенство 1,4х1 + 1,1х2 ≤11

Для начала построим прямую l3 : 1,4х1 + 1,1х2 =11

Находим две любые точки, принадлежащие прямой.

Пусть х1 = 0, тогда х2 = 10. Получили точку (0;10)

Пусть х2 = 0, тогда х1 = 7,9. Получили точку (7,9;0)

Чтобы узнать, какую полуплоскость - верхнюю или нижнюю по отношению к прямой - задает неравенство, подставим в неравенство значение какой нибудь точки. Например (0;0) : 1,4*0 + 1,1*0 = 0, 0 ≤11, т.е. берем ту полуплоскость, которая содержит (0;0), т.е. нижнюю.

. Условия 2,4≤х1 и 0,7≤х 2 означают, что мы будем рассматривать только значения х2 большие 0,7 и х1 большие 2,4.

Тогда система неравенств будет задавать ОДР, которая получится в пересечении трех полученных полуплоскостей и расположенная в данной полосе. Мы получили многоугольник АВСД - так называемый многоугольник решений.

Решением системы неравенств будут координаты всех точек, принадлежащих ОДР, т.е. многоугольнику АВСД. Но поскольку в образовавшейся ОДР бесчисленное множество допустимых решений и, как следствие, не все они будут оптимальными.

Могут быть предложены следующие подходы для нахождения оптимальных решений:

F1 = х1 + х2х - максимизировать суммарный выпуск продукции.

F2 =16,3 х1 +9,9 х2х - максимизировать прибыль.

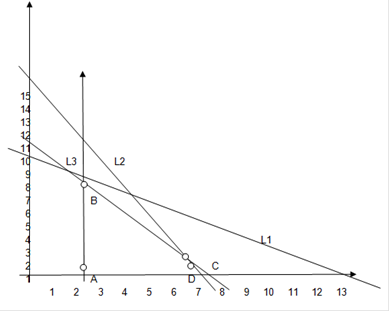
Рис 1. График определения области допустимых решений (ОДР)

Найдем координаты вершин многоугольника.

Координаты т.А : (2,4;0,7)

Координаты т.В пересечение прямой х1=2,4 и прямой L3

х1=2,4

,4х1 + 1,1х2 =11

х1=2,4

х2 =6,9

Координаты т.С - пересечение прямых L2 и L3

Получаем систему уравнений:

х1 + 2х2 =30

,4х1 + 1,1х2 =11

х1= 6,9

х2=1,2

Координаты т.Д пересечение прямой х2=0,7 и прямой L2.

х2=0,7

х1 + 2х2 =30

х2=0,7

х1= 7,2

Таблица 2. Решение задачи распределения ресурсов

Еще статьи по теме

Снижение уровня загрязненности рек г. Новокузнецка
С помощью системного анализа можно исследовать различные социально-экономические процессы и системы для лучшего понимания проблемы и поиска мероприятий по ее разрешению. В данной расчетной работе мы с помощью методов системного анализа рас ...

Проблемы экологизации сельского хозяйства
Современное сельское хозяйство является высокоразвитой отраслью деятельности человека, которая оказывает огромное воздействие на окружающую среду. Сельское хозяйство нашей страны имеет высокоразвитое животноводство. Крупные животноводчески ...